When building a regression model with categorical variables with more than two levels (ie “Cold”, “Freezing”, “Warm”) R is doing internally some transformation to be able to compute regression coefficient. What R is doing is that it is turning your categorical variables into a set of contrasts, this number of contrasts is the number of level in the variable (3 in the example above) minus 1. Here I will present three ways to set the contrasts and depending on your research question and your variables one might be more appropriate than the others.
# setting seed so that numerical results stay stable
set.seed(25)
# let's imagine an experiment which measure plant biomass based on various
# levels of nutrient added to the medium first case one treatments three
# levels
f <- gl(n = 3, k = 20, labels = c("control", "low", "high"))
# with treatments contrasts (default)
mat <- model.matrix(~f, data = data.frame(f = f))
# this tell us which contrast has been used to generate the model matrix
attr(mat, "contrasts")
## $f ## [1] "contr.treatment"
# simulate some ys beta <- c(12, 3, 6) #these are the simulated regression coefficient y <- rnorm(n = 60, mean = mat %*% beta, sd = 2) m <- lm(y ~ f) summary(m)
## ## Call: ## lm(formula = y ~ f) ## ## Residuals: ## Min 1Q Median 3Q Max ## -4.350 -1.611 0.161 1.162 5.201 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 11.498 0.463 24.84 < 2e-16 *** ## flow 3.037 0.655 4.64 2.1e-05 *** ## fhigh 6.163 0.655 9.41 3.3e-13 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 2.07 on 57 degrees of freedom ## Multiple R-squared: 0.609, Adjusted R-squared: 0.595 ## F-statistic: 44.3 on 2 and 57 DF, p-value: 2.45e-12
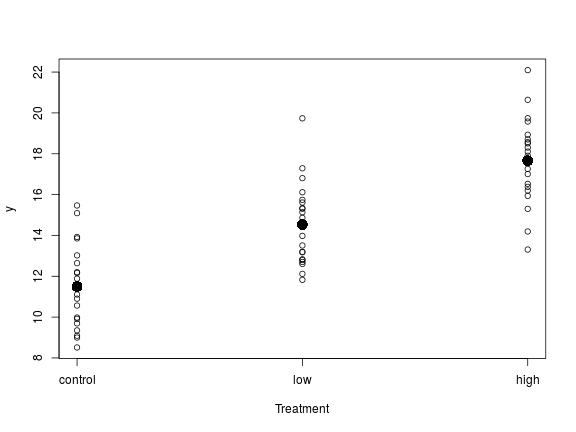
The first coefficient, the intercept, is the estimated average for the baseline group, which in our case is the control group (in the control group the biomass is estimated to be on average 11.49). The second coefficient “flow” is the estimated difference between the average in the baseline group and the average in the “low” group (this group has an increase in 3.03 biomass compared to the control group). Similarly the third coefficient is the difference between the average in the baseline and the “high” group (this group has an increase of 6.16 biomass compared to the control group).
# plot the results plot(y ~ rep(1:3, each = 20), xaxt = "n", xlab = "Treatment") axis(1, at = c(1, 2, 3), labels = levels(f)) points(c(1, 2, 3), c(coef(m)[1], coef(m)[2:3] + coef(m)[1]), pch = 16, cex = 2)
This is by default, now let’s turn to other contrasts options:
# now with helmert contrasts
mat <- model.matrix(~f,data=data.frame(f=f),
contrasts.arg = list(f = "contr.helmert"))
mat <- attr(mat, "contrasts")
## $f
## [1] "contr.helmert"
One way to set contrasts is to use the “contrast.arg” argument when building the model matrix.
# simulate the ys beta <- c(5, 3, 2) y <- rnorm(n = 60, mean = mat %*% beta, sd = 1.5) # model m <- lm(y ~ f, contrasts = list(f = "contr.helmert")) #there we tell the model to use helmert contrast to build the model summary(m)
## ## Call: ## lm(formula = y ~ f, contrasts = list(f = "contr.helmert")) ## ## Residuals: ## Min 1Q Median 3Q Max ## -2.281 -0.973 -0.202 0.752 2.986 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 4.756 0.184 25.9 <2e-16 *** ## f1 3.116 0.225 13.9 <2e-16 *** ## f2 1.949 0.130 15.0 <2e-16 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 1.42 on 57 degrees of freedom ## Multiple R-squared: 0.88, Adjusted R-squared: 0.876 ## F-statistic: 209 on 2 and 57 DF, p-value: <2e-16
Now the meaning of the various coefficient is different, the intercept is the average biomass over all the levels (across control, low and high), f1 is the difference between the average of the first level (control) and the average of the second one (low), plants in the treatment low have a 3.11 increase in biomass. f2 is the difference between the average of control and low and the average of high treatment. To put this differently, if we put together the data from the control and low treatment and compare there average value to the average value of plants in the high treatment we would get fhigh. Mean biomass of the plants in the high treatment is higher by 1.95 than plants of the control and low treatment. This type of contrast is a bit harder to interpret but is well suited for variables where the levels have an order, ie (“0”,“>0 and 5 and <10” …), there we can gradually compare the successive levels.
As a note, in most applied cases we can set the contrasts that will be used by the model using contrasts(factor)<-'some_contrasts'. Let's turn to the last contrasts the effect (or deviation) coding:
# now with sum contrasts, let's spice up a little bit and introduce an
# interaction with a continuous variables
x <- runif(60, -2, 2)
levels(f) <- c("North", "South", "Center") #let's make different level which cannot easily be given an order or a baseline
mat <- model.matrix(~x * f, data = data.frame(f = f), contrasts.arg = list(f = "contr.sum"))
attr(mat, "contrasts")
# simulate the ys beta <- c(5, -2, 3, 2, 1, -4) y <- rnorm(n = 60, mean = mat %*% beta, sd = 1.5) # model m <- lm(y ~ x * f, contrasts = list(f = "contr.sum")) summary(m)
## ## Call: ## lm(formula = y ~ x * f, contrasts = list(f = "contr.sum")) ## ## Residuals: ## Min 1Q Median 3Q Max ## -3.271 -1.021 -0.165 0.867 3.914 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 5.057 0.207 24.42 < 2e-16 *** ## x -1.869 0.185 -10.13 4.4e-14 *** ## f1 2.699 0.295 9.16 1.4e-12 *** ## f2 2.351 0.293 8.03 8.8e-11 *** ## x:f1 0.954 0.264 3.61 0.00067 *** ## x:f2 -4.269 0.268 -15.92 < 2e-16 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 1.58 on 54 degrees of freedom ## Multiple R-squared: 0.922, Adjusted R-squared: 0.914 ## F-statistic: 127 on 5 and 54 DF, p-value: <2e-16
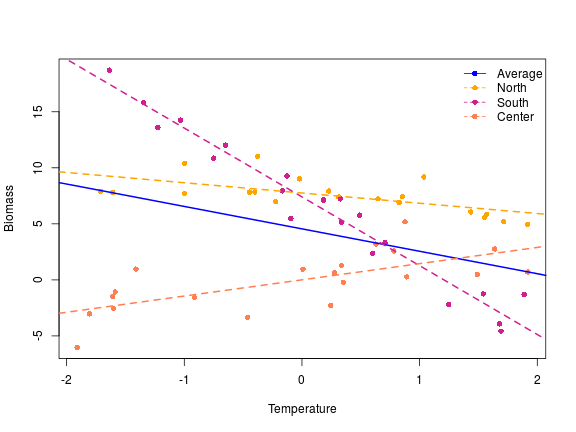
This type of contrasts is useful when there is no natural way to set a baseline or an ordering in the different levels of the variables. I changed the name of the level to illustrate what I mean by this, let’s imagine in this context that we had sampled our plant in three different localities, it is hard to determine in this context what should be the baseline, the deviation coding is a nice way to model these type of data. The intercept in this context is the overall mean across the levels (as in the helmert contrasts), so overall the plant biomass was 5.05. The second one the the average slope between the biomass and the x variable, if we increase x by one the plant biomass decrease by 1.87 across the geographical gradient. f1 is the difference between the overall mean and the mean in the north locality, similarly f2 is the difference between the overall mean and the south locality. To get the estimated average value at the center locality we have to do:
coef(m)[1] - coef(m)[3] - coef(m)[4] ## (Intercept) ## 0.00678
The interaction coefficient are the deviation of the slope within a group from the overall slope, therefore in the north if we increase x by 1, we decrease the biomass by -1.87+0.95= -0.92, similarly the slope in the south is -1.87+(-4.27)= -6.14 and in the center: -1.87-(+0.95)-(-4.27) = +1.45. Around each of these coefficient we have some assessment of the significance of the difference between the overall mean and the various groups. So far I could not find a way to assess the significance of the difference between the overall mean and the last group …
Let’s do a nice figure of this:
# a nice plot
plot(y ~ x, xlab = "Temperature", ylab = "Biomass", pch = 16, col = rep(c("orange",
"violetred", "coral"), each = 20))
abline(a = 4.55, b = -2, lwd = 2, lty = 1, col = "blue")
abline(a = coef(m)[1] + coef(m)[3], b = coef(m)[2] + coef(m)[5], lwd = 2, lty = 2,
col = "orange")
abline(a = coef(m)[1] + coef(m)[4], b = coef(m)[2] + coef(m)[6], lwd = 2, lty = 2,
col = "violetred")
abline(a = coef(m)[1] - coef(m)[3] - coef(m)[4], b = coef(m)[2] - coef(m)[5] -
coef(m)[6], lwd = 2, lty = 2, col = "coral")
legend("topright", legend = c("Average", "North", "South", "Center"), col = c("blue",
"orange", "violetred", "coral"), pch = 16, lty = c(1, 2, 2, 2), bty = "n")
That’s it for today, this page was greatly helpful in understanding the meaning of the various contrasts: http://www.unc.edu/courses/2006spring/ecol/145/001/docs/lectures/lecture26.htm, the wikipedia page is also rather nice on this: https://en.wikipedia.org/wiki/Categorical_variable

the third code box is incomplete ( beta y m |t|)).
Thanks for your vigilance, this has been now corrected.
Really good post!
A couple of comments and questiosn:
* Shouldn’t the part for the interaction in the north be -1.87-0.95= -2.82 (not 1.87-0.95= 0.92, as in the text)? The coefficient for x is negative.
* In the interactions, I understand that the intercept corresponds to the mean across samples from any condition so that
mean(y) should be very close to coefficients(m)[1] (hence the error term). Similarly, for f1 and f2 I can approximate their coefficients by taking the mean of y for samples that correspond to north (or south) and substract the global mean, thus approaching these coefficients:
mean(y[f==”North”])-mean(y) coefficients(m)[3]
mean(y[f==”South”])-mean(y) coefficients(m)[4]
How would you approach the coefficient for x ( coefficients(m)[2])?
Another thing I’m confused about is that what do x and y represent in this case, it can’t be biomass because it has negative and/or very small values (ranges from around -2 to 2). Similarly, y has negative values.
Hi jrm, thanks for spotting the mistake, I corrected the post! Concerning the second question I am not sure to get what you wrote. In the last example model the intercept (coeffcient(m)[1]) is the estimated mean in y for x=0, the second coefficient (coefficient(m)[2]) is the average increase in y for an increase in 1 unit of x. The third and fourth coefficient are the estimated deviation for the “North” and “South” group from the first coefficient when x=0. Similarly the last two coefficient are the deviation for the “North” and “South” groups from the slope coefficient.
Finally x and y can represent anything, I talked about biomass because I am familiar with this, note that if you transform/standardize biomass data you can very well get negative values.
Hope this helped.
Hello, in your test dataset by using contr.treatment as your contrasts you get the comparisons between “high” and “control” (fhigh) and “low” and “control” (flow). What if I wanted to also check the comparison between “high” and “low”? Thanks in advance for your reply. Makis
Thank you for providing this explanation and code on contrasts. It is very useful/informative. Statistics (and probably biology too) is fun! I ran into an issue with replicating the explanation for the estimates regarding the helmert contrast. The estimate above for f1 is not ‘the difference between the average of the first level (control) and the average of the second one (low)’. It looks like f1 is actually the difference between the average of (the first and second level results) and the average of the first level (control). In code: mean(y[1:40]) – mean(y[1:20]). A reference from UCLA showed how to code a custom matrix to get the results you are describing here.
Example:
my.rev.helmert<-matrix(c(-1/2,1/2,0,-1/3,-1/3,2/3),ncol=2)
contrasts(temp$f) = my.rev.helmert
summary(lm(y ~ f))
mean(y[21:40])-mean(y[1:20])
UCLA Reference:
https://stats.idre.ucla.edu/r/library/r-library-contrast-coding-systems-for-categorical-variables/